0. 概述

在 Go 中，自带的数据结构不多，其中，堆 (heap) 是其中一个，本文就先介绍一下如何使用 Go 语言中的堆，然后看它是怎么实现的。

1. heap 的使用

根据 heap 的官方文档，heap 的使用方式为：

  1. [root@liqiang.io]# cat heap_sample00.go
  2. heapObj := MinHeap{}
  3. heap.Init(&heapObj)
  5. heap.Push(&heapObj, &Item{Value: 1, Priority: 1})
  6. item := heap.Pop().(*Item)

这里有四个操作，分别是：

这里有一些关键的地方，分别是：

这里先解答第一个问题，这个 Object 要怎么实现，根据 Heap 的文档，要实现的 Interface 为：

  1. [root@liqiang.io]# cat interface.go
  2. type Interface interface {
  3.     sort.Interface
  4.     Push(x interface{}) // add x as element Len()
  5.     Pop() interface{}   // remove and return element Len() - 1.
  6. }

sort.Interface 就很简单了，有三个函数需要实现，分别是：

  1. [root@liqiang.io]# cat sort.go
  2. type Interface interface {
  3.     Len() int
  4.     Less(i, j int) bool
  5.     Swap(i, j int)
  6. }

Push 方法

Push 方法和 Pop 方法需要着重介绍一下，因为他们有一些隐藏的知识。

如果你是用树组来实现 Heap 的话，那么你需要保证插入的元素是处于最后位的。所以一个简单的实现是这样的：

  1. [root@liqiang.io]# cat push.go
  2. func (h *MaxHeap) Push(x interface{}) {
  3.     *h = append(*h, x.(*Item))
  4. }

Pop 方法

Pop 就有更多的规矩了，首先得保证 Pop 完之后，数组的元素是要少一个的，长度也要减掉，这个是由我们自己来实现的；然后，需要注意的是，heap 包已经帮我们把要移除的元素放在了最后，所以，只需要把最后一个元素返回去就可以了。

一个示例为：

  1. [root@liqiang.io]# cat pop.h
  2. func (h *MinHeap) Pop() interface{} {
  3.     x := (*h)[len(*h)-1]
  4.     *h = (*h)[0 : len(*h)-1]
  5.     return x
  6. }

2. heap 的实现

可能让你实现这个 Interface 你会觉得很不习惯，因为不理解为什么 heap 要这么做，所以，一个最好的方式还是结合 heap 的源码来看一下才更好一些。

2.1 init 函数

首先，先来看下 Heap 的 Init 做了什么事情：

  1. [root@liqiang.io]# cat init.go
  2. func Init(h Interface) {
  3.     // heapify
  4.     n := h.Len()
  5.     for i := n/2 - 1; i >= 0; i-- {
  6.         down(h, i, n)
  7.     }
  8. }

2.2 down 函数

可以看到，这里从 (n / 2 - 1) -> 0 ，每个位置都调用一下 down，那么先看这个 down 函数是什么，再理解一下这个含义：

  1. [root@liqiang.io]# cat down.go
  2. func down(h Interface, i0, n int) bool {
  3.     i := i0
  4.     for {
  5.         j1 := 2*i + 1
  6.         if j1 >= n || j1 < 0 { // j1 < 0 after int overflow
  7.             break
  8.         }
  9.         j := j1 // left child
  10.         if j2 := j1 + 1; j2 < n && h.Less(j2, j1) {
  11.             j = j2 // = 2*i + 2  // right child
  12.         }
  13.         if !h.Less(j, i) {
  14.             break
  15.         }
  16.         h.Swap(i, j)
  17.         i = j
  18.     }
  19.     return i > i0
  20. }

可以看到，所谓的 down，其实就是不断得找当前节点的子节点，然后比较是否比子节点小，如果是，那么就和子节点交换位置，否则，结束。

那么这有什么意思？很明显，其实是一个递归的思想，所谓堆，只要根节点是最小的就可以了，那么，从叶子节点开始，如果每个父节点都比子节点小，那么不就保证了根节点是最小的了么？用数学公式表达为：

i4 < i8
i2 < i4
i1 < i2
i0 < i1

即可推导出

i0 < i1 < i2 < i4 < i8

所以 i0 即是最小的。

2.3 Push

在前面使用的描述中说到了往 heap 中插入一个元素，其实就是需要把他放到树组的最后面，然后交给标准库就完成，那么，其实标准库要完成的工作就很明确了，就是如何保证这个元素插入后，heap 依旧保持特性。

这里的标准库操作很简单那，两行代码：

  1. [root@liqiang.io]# cat push.go
  2. // Push pushes the element x onto the heap.
  3. // The complexity is O(log n) where n = h.Len().
  4. func Push(h Interface, x interface{}) {
  5.     h.Push(x)
  6.     up(h, h.Len()-1)
  7. }

所以这里的关键还是 up 函数。

2.4 up

up 函数和 down 函数相对，down 是将一个元素不断得与自己子节点对比，从而实现父节点肯定比子节点小；而 up 函数则反过来，不断得将子节点与父节点对比，从而保证子节点比父节点大，代码为：

  1. [root@liqiang.io]# cat up.go
  2. func up(h Interface, j int) {
  3.     for {
  4.         i := (j - 1) / 2 // parent
  5.         if i == j || !h.Less(j, i) {
  6.             break
  7.         }
  8.         h.Swap(i, j)
  9.         j = i
  10.     }
  11. }

2.5 Pop 函数

那么怎么删除一个元素呢？确定一个删除的元素非常简单，就是树组的第一个元素就是要删除的元素了，那么，删除掉这个元素之后该如何保证 heap 的有效性呢？

删除掉元素之后，其实问题就在于根结点是空的，如果用子节点来补，那么子节点又空了，如果一直补下去，那么很容易造成 heap 的有效性丢失，即不再是一个完全二叉树。例如，可能是这么一种情况：
图 1：错误的删除方法导致堆变性

一个比较好的删除策略就是，删除一个元素之后，将最后一个元素补上来，然后再执行 down 操作，这样，就保证了这是一棵完全二叉树：
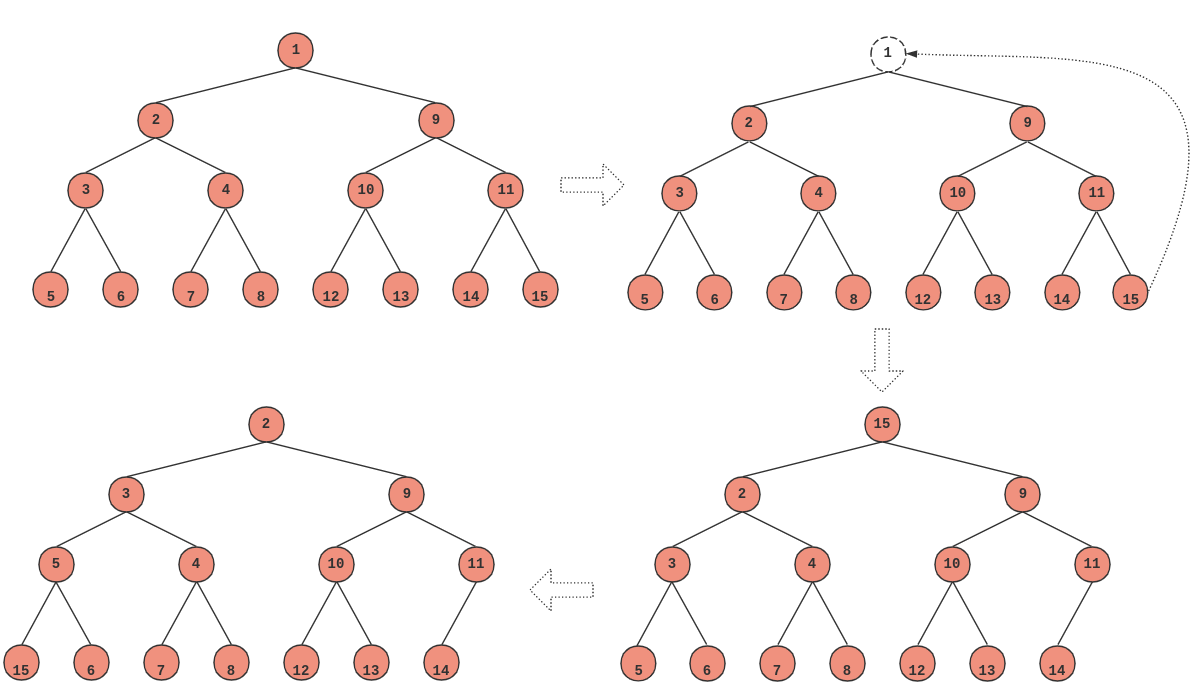
图 2：堆的正确删除姿势

可以看出，堆的删除复杂度是 log2n

3. 小结

从前边的分析可以看出，堆只需要保证偏序即可（即只需要保证父节点和子节点之间的顺序，而不需要考虑兄弟节点之间的顺序），这提高了排序的速度，所以有一种排序算法叫做堆排序，他的时间复杂度是 Nlog2N，其实就是一个 init 再加上 N 个 Pop 操作，其中：

额外补充一个：